3. Dibujar

En este apartado conoceremos las figuras primitivas e iremos agregándolas a un ejemplo en el construiremos paso a paso un dibujo. Finalizado este apartado y el siguiente de color, podremos comprender como se genera el siguiente sketch:

3.1. Coordenadas

Ya vimos como crear nuestro lienzo y ponerle un color de fondo. Ahora hay que saber cómo interpretarlo, por que va a ser necesario explicarle a p5.js donde queremos las cosas que dibujemos.

El lienzo que creamos se debe comprender como un sistema de coordenadas X e Y. El eje X es el horizontal y el eje Y es el vertical.

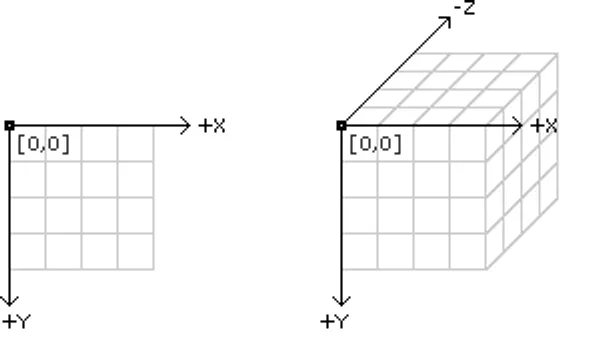
También hay que comprender que en p5.js el origen de este eje se encuentra en la esquina izquierda superior de la ventana.

Además, si trabajamos en tres dimensiones tendremos un nuevo eje de coordenadas que será el Z e indicará la profundidad.

3.2 Pixels

Como dijimos anteriormente, una pantalla de una pc es una grilla de pequeños elementos que brillan, que denominamos pixeles.

Las pantallas pueden encontrarse en muchas resoluciones: 800x600, 1024x768, 1280x1024, etc.

Estos tamaños definen la cantidad de pixeles que tiene una pantalla, y que justamente nos va a dar a nosotros una idea de la cantidad de puntos que podemos colorear.

Las imágenes en una pc son dibujadas pixel por pixel . Mientras más cantidad de pixeles, y más pequeños sean, podemos dibujar más cosas y con mayor definición.

Las resoluciones también se pueden medir por cantidad de pixeles por pulgada, lo que da una idea de con qué resolución podemos crear una imagen.

3.3 Posición

Una posición de la pantalla está comprendida por el eje de coordenadas X y el eje de coordenadas Y. El eje de coordenadas X es la distancia horizontal desde el origen y el eje de coordenadas Y es la distancia vertical.

Como dijimos anteriormente, en p5.js, el origen es la esquina superior izquierda de la ventana de representación y coordina los valores hacia abajo y hacia la derecha. La imagen de la izquierda muestra el sistema de coordenadas, y la imagen de la derecha muestra varias posiciones en la rejilla:

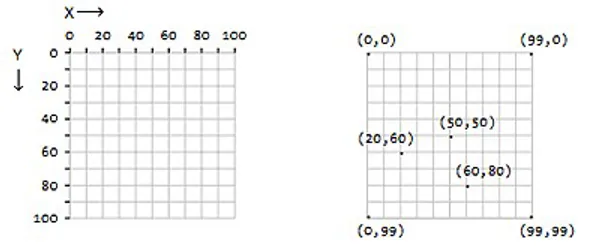
Una posición se escribe con el valor del eje X seguido del valor del eje Y, separados por una coma. La notación para el origen es (0,0), la coordenada (50,50) tiene 50px de coordenada X y 50px de coordenada Y, y la coordenada (20,60) tiene 20px de coordenada X y 60px de coordenada Y. Si el tamaño de nuestro lienzo es de 100 píxeles de ancho y 100 píxeles de alto, el píxel de la esquina superior izquierda es (0,0), el píxel de la esquina superior derecha es (99,0), el píxel de la esquina inferior izquierda es (0,99), y el píxel de la esquina inferior derecha es (99,99) . Esto se verá más claro en el punto siguiente cuando usemos la función point().

3.4 Figuras primitivas

En p5.js podemos contar con muchas funciones que se denominan primitivas.

Las funciones primitivas de los lenguajes de programación son las que poseen una conformación básica y resuelven problemas básicos.

Además en geometría se denomina primitivas a las figuras que tienen una constitución de forma básica (círculos, cuadrados, líneas, etc.)

En muchos lenguajes de programación dibujar figuras en una pantalla puede volverse dificultoso debido a que un programa debe manejar la pantalla, la placa de video y además realizar muchas acciones para mostrar adecuadamente el dibujo.

En p5.js estos problemas están en su mayoría resueltos, y en la mayoría de los casos solo tenemos que preocuparnos por el diseño y la ubicación de las cosas.

Con pocas líneas de código se pueden hacer muchas cosas que con otros lenguajes sería muy difícil de realizar.

3.5 Point

En primera instancia podemos dibujar un punto, que es el elemento visual más simple de encontrar.

Para esto utilizamos la siguiente función:

point(x,y);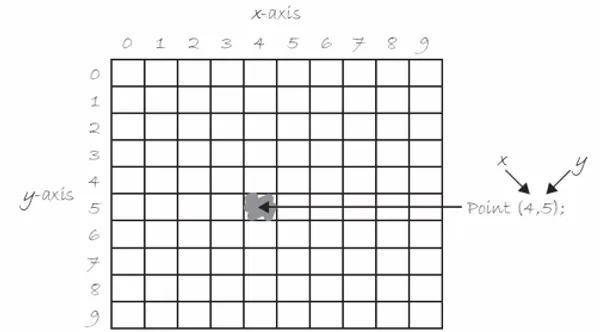

Esta función tiene dos parámetros: el primero es la coordenada X y el otro es la coordenada Y.

Un punto es del tamaño de un sólo píxel, mas adelante veremos como cambiar el tamaño en caso que lo necesitemos

Para tener en cuenta: Hay puntos dibujandose por fuera de nuestro lienzo. Por más que no los veamos estos puntos se están dibujando, solo que no se muestran.

3.6 Line

Una línea no es más que una serie de puntos. Es posible dibujar cualquier línea mediante puntos, pero p5.js tiene una función que simplifica esto: la función line(). Esta función tiene cuatro parámetros, dos por cada extremo:

line(x1, y1, x2, y2);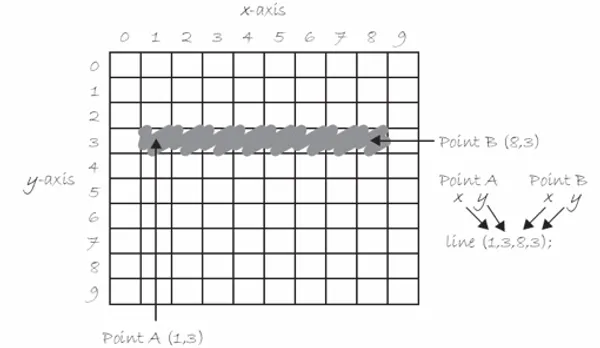

Los primeros dos parámetros establecen el punto donde la línea empieza y los dos últimos establecen la posición donde la línea termina. Con la información de esos dos puntos, p5.js se encarga de dibujar la línea que los une.

Para Jugar: probá comentar las líneas de a una para reconocer cuál desaparece y saber cuál es cada una.

3.7 Rect

Los rectángulos se dibujan de una manera un poco diferente a las líneas. En lugar de definir cada punto, los cuatro parámetros establecen la posición y las dimensiones de la figura. La función rect() dibuja un rectángulo:

rect(x, y, ancho, alto);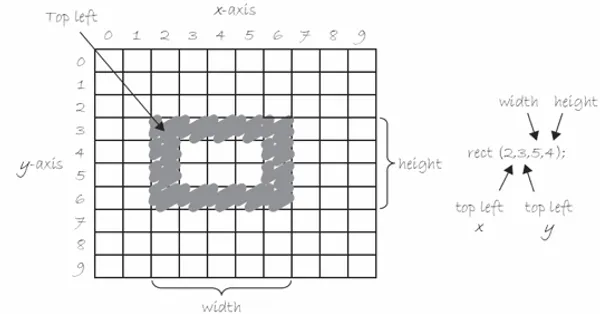

Los dos primeros parámetros establecen la localización del punto superior izquierdo, el tercero establece el ancho, y el cuarto el alto. Usando el mismo valor de ancho y alto se dibujará un cuadrado.

Para Tener en cuenta: rectángulos con mismo valor de ancho y alto forman cuadrados. Con mayor valor de alto forman un rectángulo vertical. Con mayor valor de ancho forman rectángulo horizontal

También se pueden generar rectángulos con bordes redondeados agregando nuevos parámetros a la función de la siguiente forma:

rect(x, y, ancho, alto, radio)
rect(x, y, ancho, alto, si, sa, id, ii)

El parámetro radio corresponde al radio de redondeo. La versión con otros cuatro parámetros permite agregar un radio distinto de redondeo a cada esquina. Siendo si (superior izquierdo), sa (superior derecho), id (inferior derecho) e ii (inferior izquierdo).

3.8 Ellipse

Las elipses también se dibujan de forma diferente. los cuatro parámetros establecen la posición del centro de la figura y las dimensiones de ancho y alto. La función ellipse() dibuja una elipse en el lienzo:

ellipse(x, y, ancho, alto);

Los dos primeros parámetros establecen la localización del punto del centro de la elipse, el tercero establece el ancho de la elipse, y el cuarto la altura. Usando el mismo valor de ancho y de alto se dibujará un círculo.

Los valores de ancho y alto hacen referencia a el total de pixeles de ancho y alto de nuestra figura. Como esta se calcula desde el punto central, si por ejemplo ponemos un valor de 100px de ancho, nuestra figura ocupará 50px de ancho hacia la izquierda del punto central y 50px a la derecha. Lo mismo ocurrirá con el alto.

Reemplacemos los puntos por círculos en nuestro ejemplo:

Para Tener en cuenta: Como dijimos con los puntos podemos dibujar figuras por fuera de nuestro lienzo y solo se mostrará la parte que ingrese en la ventana que hayamos creado. Este ejemplo se ve claramente con los puntos.

3.9 Triangle

La función triangle() dibuja un triángulo. Tiene seis parámetros, dos por cada punto, que representan cada uno de los vértices del triángulo:

El primer par define el primer punto, el segundo par el segundo punto y el último par el tercer punto. Cualquier triángulo puede ser dibujado conectando tres líneas, pero la función triangle() hace posible dibujar una figura con relleno. Triángulos de todas formas y tamaños pueden ser creados cambiando los valores de los parámetros.

Para Jugar: probá comentar todo el resto del código con los caracteres de apertura /* y de cierre */ para reconocer solo los triángulos.

3.10 Quad

La función quad() dibuja un cuadrilátero, osea, un polígono de cuatro lados. Funciona de manera similar a los triángulos, ya que debemos establecer la ubicación de cada uno de los cuatro vértices. Por lo tanto, tiene ocho parámetros dos por cada punto:

Variando los valores de los parámetros se puede construir rectángulos, cuadrados, paralelogramos y cuadriláteros irregulares.

3.11 Bezier

La función bezier() puede dibujar líneas que no son rectas. Una curva Bézier está definida por una serie de puntos de control y puntos de anclaje. Una curva es dibujada entre dos puntos de anclaje, y los puntos de control definen su forma:

Esta función requiere ocho parámetros para definir cuatro puntos. La curva se dibuja entre el primer punto y el cuarto, y los puntos de control están definidos por el segundo y tercer punto.

En los programas que se utilizan curvas Bézier, tales como Adobe Illustrator o Inkscape, los puntos de control son representados por pequeños nodos que sobresalen de los bordes de la curva.

3.12 Orden de dibujo

El orden en que dibujamos las figuras en el código, define qué figuras aparecerán sobre otras en la ventana de representación. Como dijimos anteriormente, el editor lee las instrucciones una a una de arriba abajo, por lo tanto, si dibujamos un rectángulo en la primera línea de un programa y una elipse en la segunda línea, el rectángulo aparecerá debajo de la elipse cuando ejecutemos el programa, ya que primero se dibujara el rectángulo y luego la elipse. Revirtiendo el orden, el rectángulo se coloca arriba.

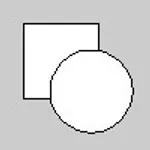
rect(15, 15, 50, 50); //Abajo
ellipse(60, 60, 55, 55); //Arriba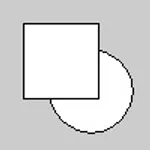

ellipse(60, 60, 55, 55); //Abajo
rect(15, 15, 50, 50); //Arriba

3.13 Contornos de Figuras

Las figuras tienen una línea que configura su contorno. Los atributos de esta línea, están controlados por las funciones strokeWeight(), strokeCap() y strokeJoin().

Cuando se escriba alguna de estas funciones afectarán a todas las figuras que se encuentren en las líneas posteriores de nuestro código, hasta que indiquemos otra cosa volviendo a asignarle un valor.

La función strokeWeight() tiene un parámetro numérico que define el grosor en pixeles del contorno de las figuras. Cuando afecta a la función line() indicará el grosor de nuestra línea y con la función point() el tamaño de nuestro punto.

La función strokeCap() determina los puntos finales de las líneas. Recibe un solo parámetro que puede ser ROUND, SQUARE o PROJECT.

ROUND redondea los puntos finales, SQUARE los vuelve cuadrados y PROJECT las extiende. Esta función se usa en líneas.

Si no se escribe la función, se utiliza por defecto el valor ROUND.

La función strokeJoin() determina la forma en la que se unen los vértices de las figuras. Recibe un solo parámetro que puede ser BEVEL, MITTER o ROUND.

BEVEL corta en diagonal las esquinas cuadradas, MITTER cuadra las esquinas (es el valor por defecto) y ROUND redondea las esquinas.

Si no se escribe la función, se utiliza por defecto el valor MITTER.

3.14 Modos de dibujo

Cuando dibujamos elipses o rectángulos, los ubicamos como explicamos anteriormente, indicando el punto de arriba a la izquierda para los rectángulos e indicando el punto del centro para las elipses.

Esto se puede cambiar con las funciones ellipseMode() y rectMode().

ellipseMode recibe los parametros CENTER, RADIUS, CORNER y CORNERS, para definir desde donde se toma la coordenada de posición.

El modo por defecto es CENTER, cuyos parámetros se explicaron en el apartado de la función ellipse().

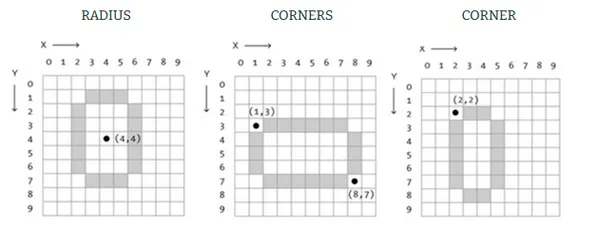
El modo RADIUS también utiliza los dos primeros parámetros para posicionar el centro, pero utiliza el tercer parámetro para definir la mitad del ancho y el cuarto parámetro para definir la mitad de la altura. De esta manera con RADIUS, los parámetros de ancho y alto definen el radio de la elipse, no el diámetro.

Con CORNER, se define la posición de la elipse desde la esquina superior izquierda. Con CORNERS se define la posición con los dos primeros parámetros desde la posición superior izquierda y la extensión de la elipse hasta las coordenadas indicadas en el parámetro 3 y 4.

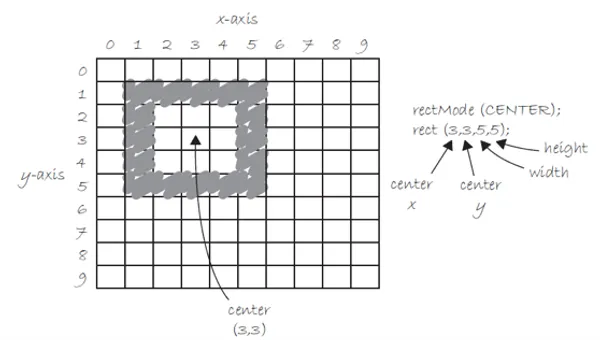
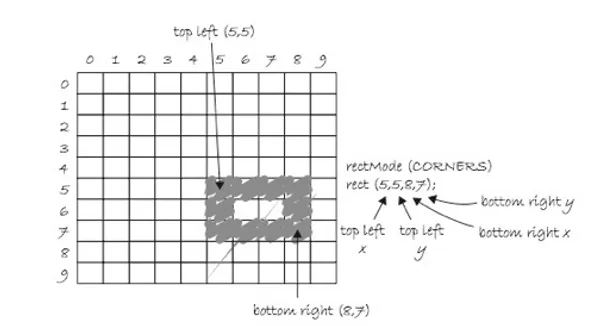
Con un estilo similar, la función rectMode() afecta a cómo se dibujan los rectángulos. Requiere un parámetro que puede ser CORNER, CORNERS o CENTER. El modo por defecto es CORNER que funciona como fue explicado en el apartado de la función rect().

CORNERS causa que el tercer y cuarto parámetro de rect() se definan en la esquina contraria a la primera. El modo CENTER causa que el primer y segundo parámetro de rect() definan el centro del rectángulo y usa el tercer y cuarto parámetro para el ancho y el alto.