1. Transformaciones

En esta clase iremos viendo diferentes conceptos de transformaciones, iteraciones y movimientos para llegar a modificar nuestro sketch haciendolo mas dinámico y escalable. Al final de la clase podremos comprender el código que realiza las acciones del siguiente ejemplo:

1.1 Transformaciones

Hasta ahora vimos como posicionar las figuras modificando los parámetros de la función que los constituye. Una técnica alternativa para posicionar y mover objetos en la pantalla es cambiar el sistema de coordenadas de la pantalla. Por ejemplo, podés mover una figura 50 píxeles a la derecha, o podés mover la ubicación de la coordenada (0,0) 50 píxeles a la derecha - el resultado visual en la pantalla es el mismo. Al modificar el sistema de coordenadas por defecto, podemos crear diferentes transformaciones incluyendo traslación, rotación, y escalamiento.

1.2 translate(), translación

La función translate() mueve el origen de la esquina superior izquierda (la cual por defecto se encuentra en el 0, 0) a otra localización. Acepta dos parámetros. El primero es la coordenada en x y el segundo en y.

translate(x, y)

Los valores de x y de y que se ingresan afectan a cualquier figura o forma que se pretenda dibujar después.

Si 10 es el parámetro de x, y 30 es el parámetro de y, un punto dibujado en la posición (0, 5) se mostrará en la posición (10, 35).

Hay que tener en cuenta que la función translate() es aditiva. Si translate(10, 30) se ejecuta dos veces, entonces la posición de base será (20, 60).

1.3 push() y pop()

Para aislar los efectos de las transformaciones para que no afecten otras funciones, se puede usar las funciones push() y pop(). Cuando se ejecuta push(), se almacena una copia del sistema de coordenadas actual y luego se puede restaurar ese sistema ejecutando pop(). Esto es útil cuando se necesita transformar una figura o un grupo de estas, pero no se quiere afectar otras.

Sirve pensarlo, para quienes manejan programas al estilo del Adobe Photoshop o GIMP, como que este nuevo sistema de coordenadas que se genera entre la llamada de push() y de pop() es tan solo una capa. A dicha capa podemos darle características diversas (trasladar, rotar, escalar).

Las funciones push() y pop() siempre se usan de a pares. Por cada push(), tiene que haber un correspondiente pop().

Al segmentar nuestras figuras con diferentes sistemas de coordenadas, se puede tener más control de todo lo que pasa en el programa.

1.4 rotate(), rotación

Otra forma en la que podemos afectar las figuras es con la función rotate() que nos permite rotar las coordenadas de un sistema, de modo tal que las figuras y formas sean dibujadas con cierto ángulo. Recibe tan solo un parámetro, el cual modifica la rotación de acuerdo a un ángulo:

rotate(angulo)

El parámetro ángulo asume que el valor se encuentra en radianes. Para convertir los ángulos en radianes hacemos uso de la función radians(), pasándole como parámetro un número que corresponde a los grados del ángulo. También se puede hacer uso de la variable PI que corresponde a un ángulo de 180 grados y las multiplicaciones y divisiones de esta.

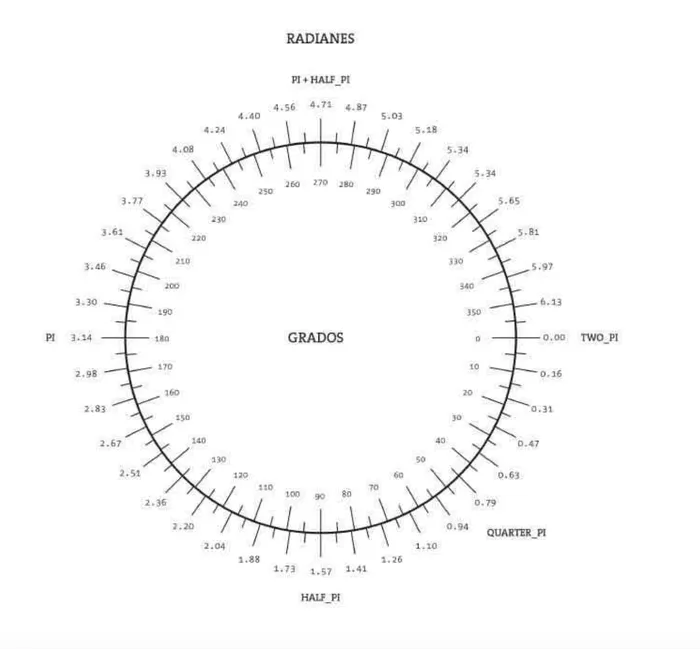
Las figuras son siempre rotadas en relación a la posición de origen (0, 0).

Como en todas las transformaciones, el efecto de rotación también es acumulativo, pero si usamos push() y pop(), podremos segmentarlo por figuras.

1.5 scale(), escala

Por otro lado, la función scale() permite controlar las coordenadas del sistemas para magnificarlas y dibujar figuras de mayor escala. Esta soporta uno o dos parámetros:

scale(tamaño)
scale(xtamaño, ytamaño)

La versión de un solo parámetro permite escalar la figura en todas sus dimensiones, mientras que la de dos parámetros abarca la escala en el eje x y en el eje y de manera individual. Los parámetros a ingresar se expresan como valores decimales con una relación de porcentajes. Por ejemplo, 2.0 hace alusión a 200%, 1.5 a 150%, y 0.5 a 50%.

1.6 Combinando transformaciones

Cuando una figura es afectada por transtale(), rotate() o scale(), siempre todo es en relación a la coordenada de origen. Por ejemplo, al rotar un rectángulo en la coordenada (50, 20), la rotación se hará sobre ese mismo eje:

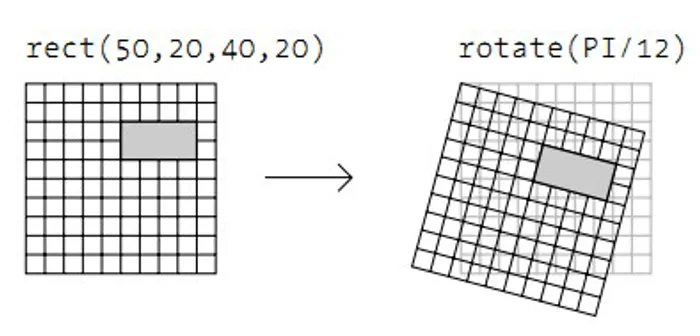
Para hacer que la figura rote sobre su propia esquina, se debe cambiar la coordenada a la posición (0, 0).

Para esto, utilizaremos la función translate(). Cuando la figura rote, lo hará sobre su esquina superior Izquierda.

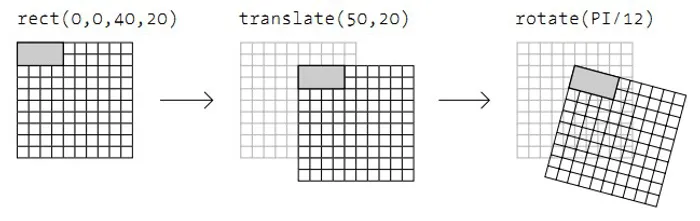
Hay dos maneras de pensar las transformaciones. Un método es utilizar las funciones para transformar, y luego corregir el problema de posición con las coordenadas propias de la figura. El otro método consiste en utilizar las propias funciones de transformación para corregir lo no deseadog3 Esto se puede ver en la sección comentada como capa 2 en nuestro ejemplo anterior.